一、黎曼猜想
 

简介
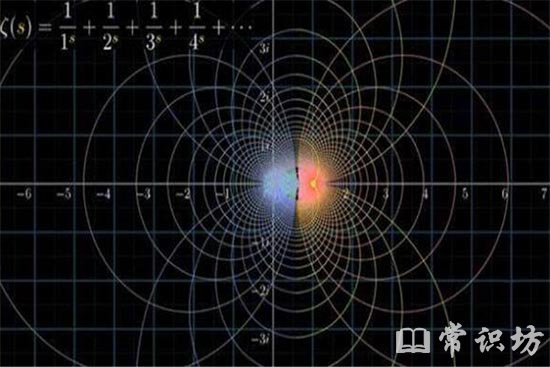
在世界七大数学难题中黎曼猜想据说是一道非常神秘的数学题，说函数等0时的时候，其中所有解在同一直线上，曾经博奕论鼻祖纳什花了不知道多少年来解这道题，结果到最后不仅没解开还疯掉了。
 
二、霍奇猜想
 

简介
霍奇猜想可以说难道几乎所有的数学家，猜想表达能够将特定的对象形状，在不断增加维数的时候粘合形成一起，看似非常的巧妙，但在实际的操作过程中必须要加上没有几何解释的部件。
 
三、BSD猜想
 

简介
BSD猜想相信不少对数学感兴趣的朋友都是有了解的，这个猜想更像是一个代数方程，但最终BSD猜想被指出是不可解的，而且如果是函数z(s)在点s=1附近的性态，会随着结果的不同有理点和有限点数都很多。
 
四、杨-米尔斯存在性和质量缺口
 

简介
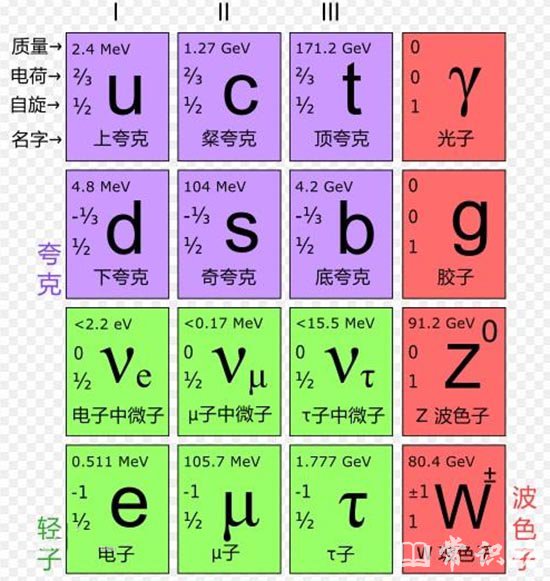
量子物理的定律是以经典力学的牛顿定律对宏观世界的方式对基本粒子世界成立的。大约半个世纪以前，杨振宁和米尔斯发现，量子物理揭示了在基本粒子物理与几何对象的数学之间的令人注目的关系。基于杨－米尔斯方程的预言已经在如下的全世界范围内的实验室中所履行的高能实验中得到证实：布罗克哈文、斯坦福、欧洲粒子物理研究所和驻波。尽管如此，他们的既描述重粒子、又在数学上严格的方程没有已知的解。特别是，被大多数物理学家所确认、并且在他们的对于“夸克”的不可见性的解释中应用的“质量缺口”假设，从来没有得到一个数学上令人满意的证实。在这一问题上的进展需要在物理上和数学上两方面引进根本上的新观念。
 
五、NP完全问题
 

简介
NP完全问题可以说是一个听着就很复杂的数学问题，简单的讲所有的完全多项式在非确定性的问题，都可以被转化为名为满足性的逻辑运算问题，数学家们猜想的是到底有没有一个确定性的算大，不过至今.....
 
六、庞加莱猜想

 
简介
庞加莱猜想提出来很长时间了，猜想中提到如果不断的去扯一个橡皮筋，然后让它慢慢于移动伸缩为一个点，最终能否证明三维球面或者是四维空间中的和原点有距离的全部问题，简直就是很困难了.....
 
七、纳卫尔-斯托可方程的存在性与光滑性
 

简介
这个数学问题本是数学家们用来研究无论是在微风还是在湍流等情况下，都能用纳卫尔-斯托可的方程式做出相应的数据解答，但是到目前能完全理解纳卫尔-斯托可方程式的人少之又少，而且有些理论的实质进展很微妙。

目录

一、黎曼猜想
二、霍奇猜想
三、BSD猜想
四、杨-米尔斯存在性和质量缺口
五、NP完全问题
六、庞加莱猜想
七、纳卫尔-斯托可方程的存在性与光滑性